seattlecros.blogg.se

1. Lambda calculus beta reduction examples how to#
2. Lambda calculus beta reduction examples full#
3. Lambda calculus beta reduction examples free#

Lambda calculus beta reduction examples free#

e 1) e 2 e 1e 2/x where the notation e 1e 2/x denotes the result of substituting e 2for all free occurrences of x in e 1. It was introduced by the mathematician Alonzo Church in the 1930s as part of his research into the foundations of mathematics. The only reduction rule of interest in this course is called beta-reduction, and is dened by: (x. It is a universal model of computation that can be used to simulate any Turing machine.

Lambda calculus beta reduction examples full#

The classical lambda calculus allows full beta reduction. Lambda calculus (also written as λ-calculus) is a formal system in mathematical logic for expressing computation based on function abstraction and application using variable binding and substitution. As the preceding examples suggest, once we have -abstraction and.

Conventionally, we prefix abstractions with a λ, taking the following form.It has been suggested that Explicit substitution be merged into this article. As we saw earlier, a function takes exactly one argument, and may return another function. Lambda abstractionĪ lambda abstraction is an anonymous function definition. In the simplest form of lambda calculus, terms are built.

Lambda calculus beta reduction examples how to#

For example: x, y, and z are all valid variables. the pure untyped lambda calculus, show how to encode numbers and algebraic data types, and define evaluators for it. Lambda calculus consists of constructing lambda terms and performing reduction operations on them. Here is the sequence of beta-reductions without the intermediate steps: (lambda x.x y)(lambda y.y z) rightarrowbeta (lambda y.y z) y rightarrowbeta y z. In λ, we typically use the convention of a single lower case letter. VariablesĪ variable is just a name that may hold a value, just as you would expect. Is my reasoning correct (Since there were no solutions to these notes, I want to ensure my understanding is correct. q), and then since there are no occurences of y in the resulting term, the expression simply evaluates to ( z.

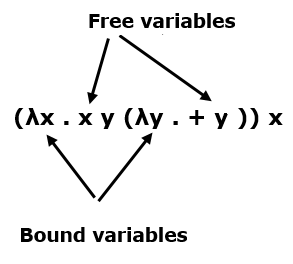
Expressions are evaluated from left to right. z) as follows: First I replace occurences of x in M by a a ( p q. There are only 3 types of expressions Īny expression may be parenthesized in order to change the evaluation order. Fortunately, these extensions are easy to add, while preserving the semantics of λ. You will not find features such as top-level named functions or variables, locally scoped variables, pattern matching, or many other features you might expect of a general purpose programming languages. An evaluation strategy is deterministic, if it allows reduction with at most one redex, for any term. As we will see later, this process is called currying. Lambda Calculus Calculator supporting the reduction of lambda terms using beta- and delta-reductions as well as defining rewrite rules that will be used in.